Valorisation pre-money et Valorisation post-money : une fausse équation ?

Contrairement aux entreprises cotées en bourse, lors de levées de fonds pour les startups, les es PME ou les ETI, la question de la dilution se pose toujours : si nous réussissons une augmentation de capital de X MEUR, quelle part du capital est acquise par les investisseurs ?

La réponse pragmatique est celle de la transaction réelle : quelle part acceptable veulent les investisseurs en échange de cette injection de cash ? Sur la base de ces éléments es déterminée la valeur des titres de l’entreprise après l’AKA (augmentation de capital), appelée « valorisation post-money ».

Et c’est là qu’intervient une fausse déduction, basée sur une hypothèse implicite d’une équation beaucoup trop simpliste : le « calcul » de la valorisation « pré-money », c’est-à-dire la valeur des titres de l’entreprise avant l’AKA.

En effet, ce qui est généralement utilisé est l’équation linéaire : Valeur pré-money = Valeur post-money – montant de l’AKA.

Or, si on ajoute la Valeur de la Dette nette aux 2 côtés de l’équation, on obtient l’égalité Valeur d’entreprise pré-money = Valeur d’entreprise post-money – montant de l’AKA.

Mais la définition officielle de la Valeur d’une entreprise est : « La valeur d’une entreprise est la valeur actuelle de ses flux futurs de trésorerie disponibles, actualisés en fonction du risque associé à ces flux. »

Donc avec cette équation simpliste, l’on dit en fait que la Valeur de l’entreprise après l’opération, la Valeur « post-money », est identique à celle pré-money, mais uniquement ajustée d’une augmentation de trésorerie égale au montant de l’AKA.

Dit autrement, l’on fait ici comme si cet apport de cash (l’AKA) n’allait pas augmenter les cash-flows futurs de façon supérieure au montant de cash apporté : il n’y aurait donc en réalité pas de création de valeur par l’entreprise permis par cette AKA !…

Cette équation simpliste est donc évidemment fausse !

Bien entendu, pour une AKA d’un montant M donné (en MEUR par exemple), lorsque la valeur pré-money augmente fortement (tend vers l’infini schématiquement), l’on se rapproche du cas où il n’y a pas de création de valeur supérieure au montant de l’AKA.

Par exemple, si le groupe français TOTAL ENERGIES, dont la valeur des titres est actuellement supérieure à 134 bn EUR (sa capitalisation boursière actuelle), décidait de faire une augmentation de capital de 1 MEUR, la valeur de ses titres (ou la valeur de l’entreprise) n’augmenterait mécaniquement que du montant de l’AKA (1 MEUR dans cet exemple « absurde »).

En revanche, pour une jeune startup, si l’on conserve le même exemple d’une AKA de 1 MEUR, cet apport de cash permettrait a priori une création de valeur supérieure au montant de l’AKA (et c’est l’espoir des entrepreneurs comme des investisseurs), et même très supérieure dans certains cas.

Dit autrement, on peut s’interroger sur la famille des fonctions f_M (x), où :

• x est la valeur des titres de l’entreprise avant l’AKA (valorisation pré-money) ;
• M est le montant de l’AKA ;
• f_M (x) est la valeur de ses titres après l’AKA (valorisation post-money).

A priori, on peut imaginer en première approche le comportement suivant :

• f_M (x) tend asymptotiquement vers y=x+M quand x tend vers l’infini ;
• f_M (x) est strictement croissante : c’est une hypothèse qui n’est évidemment pas toujours réalisée, mais cela demeure l’espoir de tous ; c’est-à-dire que, pour un montant M d’AKA donné, si une entreprise E1 a une valeur pré-money inférieure à une entreprise E2, la valeur post-money de E1 demeure inférieure à la valeur post-money de E2 ;
• f_M (x) est toujours au-dessus de y=x+1 ;
• f_M (x) a une forme de « cloche », c’est-à-dire que nous faisons l’hypothèse qu’il y a une zone de valeur pré-money où ce montant M d’AKA a un impact optimal en termes de création de valeur. Dit autrement, nous faisons l’hypothèse que la création de valeur permise par l’AKA croît au début, puis décroît après un optimum.

Ces hypothèses de comportement, tout comme la remarque initiale sur l’équation simpliste et fausse entre les 2 valeurs pré et post-money, sont notamment corroborées par le fait que l’un des indicateurs privilégiés des fonds d’investissement est le ROCE : le retour sur les capitaux engagés. En effet, un fonds d’investissement jauge la qualité de son propre travail, et celui des entrepreneurs, selon l’optimisation du ROCE :

• Est-ce que les entrepreneurs ont utilisé efficacement les capitaux injectés pour créer suffisamment de valeur ?
• Est-ce que le fonds a fait le bon choix en injectant ce montant d’AKA dans cette entreprise plutôt qu’un autre montant (ou qu’une autre entreprise) ?

Pour illustrer ces hypothèses de comportement, nous avons demandé à ChatGPT de tracer la courbe* illustrative suivante, en faisant l’hypothèse que l’AKA est de 1 MEUR :

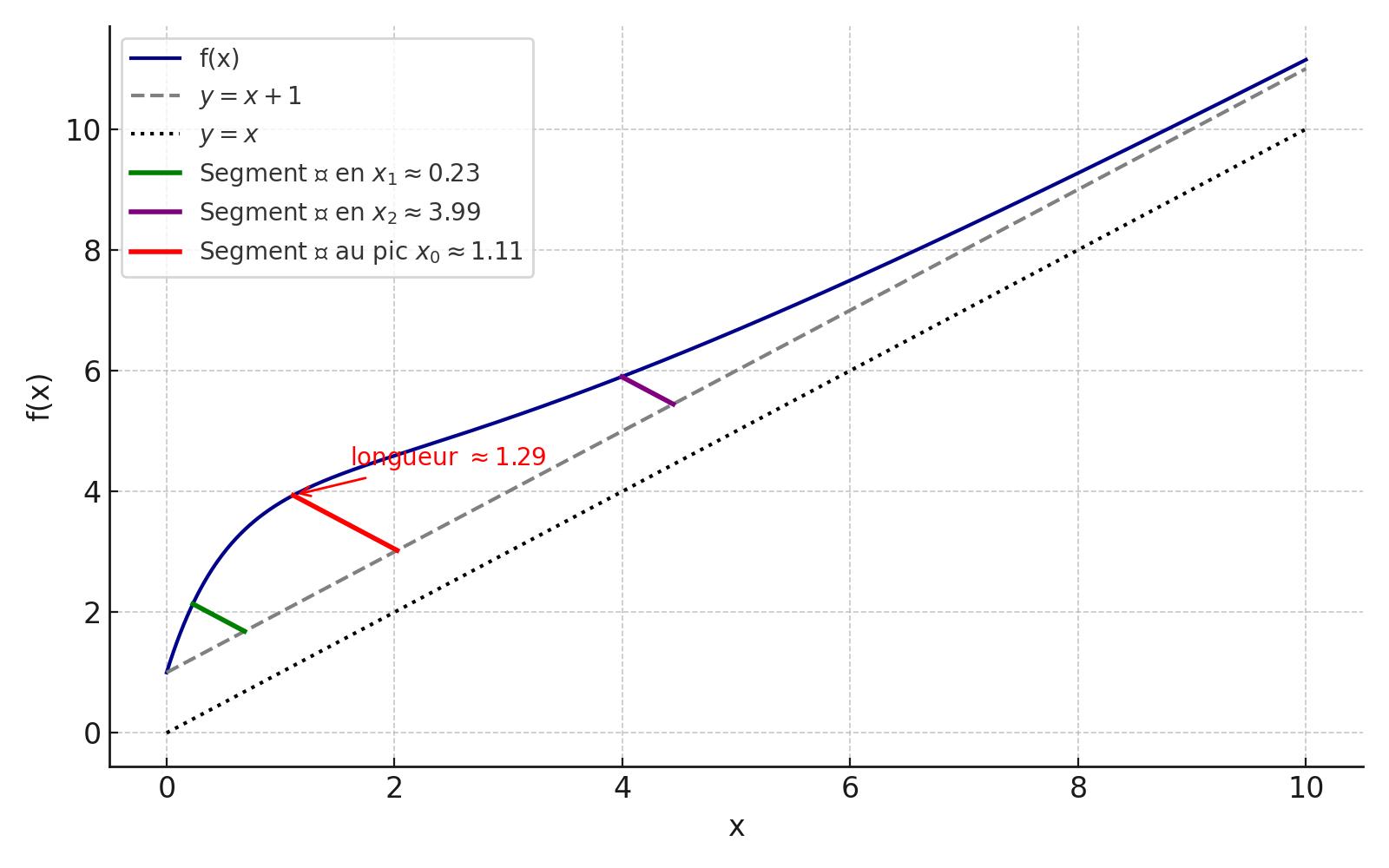
Nous obtenons notamment l’information suivante :

Le « pic de la cloche » se situe à x0 ~1,11 et vaut ~1,29. Dit autrement, l’AKA de 1 MEUR produit un résultat optimal lorsque la valorisation pré-money est autour de 1,11 MEUR, et cela porterait (dans cet exemple) la valeur post-money à 1,11 + 1 + 1,29 = 3,40 MEUR (y=x+1 + taille du pic de cloche). Dit autrement, 1 MEUR injecté dans ce cas créerait en plus 1,29 MEUR de valeur additionnelle 2,29 MEUR de création de valeur au total) : un équivalent de ROCE brut de 2,29x (calcul basique pour seule illustration).

Comment avancer de façon constructive sur la base de cette analyse ?

Tout d’abord, notons que dans l’exemple ci-dessus, les valeurs pré-money qui sont telles que la création de valeur demeure supérieure ou égale à la moitié de ce maximum sont ici environ : 0,23 MEUR et 3,99 MEUR.

Dit autrement, si la valeur pré-money réelle de la startup est proche de 0,2 MEUR, avec cette simulation, le surplus de création de valeur apportée par une AKA de 1 MEUR est estimé à 50% * 1,29, soit 0,65 MEUR. Ici, l’AKA de 1 MEUR commence à être sous-optimale : il faudrait en réalité soit procéder à une AKA inférieure, soit procéder à une AKA de 1 MEUR dans une entreprise à plus forte valeur pré-money.

Cela peut sembler logique opérationnellement : si la valeur de la startup est trop faible, cela est corrélé au fait qu’elle n’a pas encore franchi certaines étapes de son développement, et donc qu’elle ne serait pas en mesure d’utiliser convenablement de « trop grands moyens ».

Par ailleurs, cela pourrait inciter certains fonds d’investissement, ou acteurs de l’écosystème, à explorer analytiquement avec les cas réels des participations en portefeuille, la forme et les valeurs clés de certaines de ces courbes. Notamment, en profiter pour faire des REX pour vérifier si le ROCE a été au bon niveau sur les deals passés.

Ainsi, cela pourrait aider certains comités d’investissement à argumenter pour éviter certaines surenchères de prix de remises d’offres, qui, in fine, font dériver les performances des portefeuilles, et jouent des mauvais tours à l’ensemble du marché.

* Pour les amateurs de mathématiques, l’équation de f(x) proposée par ChatGPT est :

f(x) = 1 + x + 3 * (exp(-0,3 x) – exp(-2 x))